С 2022 года в ЕГЭ появилось новое задание: составление уравнения функции по графику. Основная идея решения - используя координаты точек, составить систему уравнений  и вычислить неизвестные параметры функции. Но, как и в большинстве хорошо составленных заданий, в этих заданиях тоже есть свои фишки. Именно о них поговорим подробно. Задания взяты с сайта РешуЕГЭ

1) Линейная функция.

Пример задания:

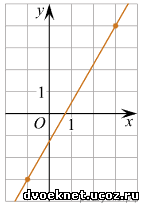
На рисунке изображён график функции f (x) = kx + b. Найдите f (- 5) . 

Решение.

1 вариант - нахождение параметров k и b через систему уравнений. Точки уже выделены на графике: (3;4) и (-1;-3). Подставим координаты точек в формулу:

4=3k+b          b=4-3k                   b=4-3k        k=7/4

-3=-k+b          -3=-k+4-3k            4k=7            b= -5/4

f(-5) = 7/4 * (-5) -5/4 = -40/4 = -10

2 вариант. Небольшой секрет. Вспомним, что угловой коэффициент k = tg(a) = y/x. 

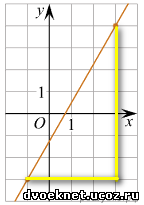
Из рисунка видно, что k = 7/4. Теперь достаточно подставить найденное значение k и координаты одной из точек графика в формулу и вычислить параметр b.

Ответ: -10

 

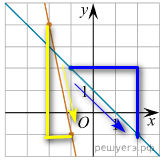
Замечание. При использовании свойств функции важно не забыть о том, что для возрастающей функции k > 0,  а для убывающей k < 0. Например, в приведенном ниже примере угловой коэффициент желтой прямой k = -5, а у синей k = -1

2) Квадратичная функция

Основной способ решения этих заданий - составление системы уравнений. 

Пример задания

На рисунке изображён график функции вида  где числа a, b и c — целые. Найдите значение .

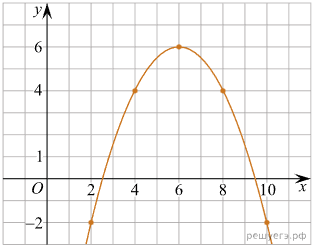
Выберем координаты трех точек графика. Например (2; -2), (4; 4), (6; 6). Подставим их в формулу функции

4/a + 2b + c = -2                   4/a = -2 - 2b - c                                   4/a = -2 - 2b - c                                  4/a = -2 - 2b - c                  4/a = -2 - 2b - c                  4/a = -2 - 2b - c                4/a = -2 - 2b - c          a = -2

16/a + 4b + c = 4                 4(-2 - 2b - c) + 4b + c = 4                   -8 - 8b - 4c + 4b + c = 4                     -4b - 3c = 12                         4b = -12 - 3c                      4b = -12 - 3c                    4b = -12 - 3c              b = 6

36/a + 6b + c = 6                 9(-2 - 2b - c) + 6b + c = 6                   -18 - 18b - 9c + 6b + c = 6                 -12b - 8c = 24                       3(-12 - 3c) + 8c = -24          -36 - c = -24                   c = -12                       c = -12

Значит, функция задана формулой f(x) = -0.5x² + 6x - 12. f(0) = -12

Ответ: -12

 

Если координата пересечения параболы с осью у является целым числом, то решение задачи можно упростить

Пример задания

На рисунке изображён график функции вида  где числа a, b и c — целые. Найдите значение .

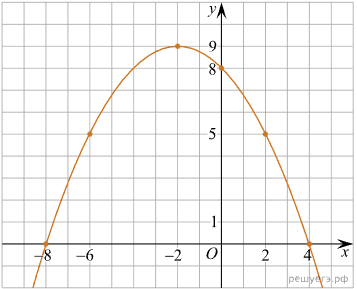
По графику видно, что при х = 0 функция равна 8. f(0) = c, значит, с = 8.

Так как параметр с легко находится устно, то достаточно подставить координаты двух точек графика для нахождения параметров а и b. Попробуйте сделать это самостоятельно. 

a =  -4, b = -1, c = 8. f(-5) = 6,75

Ответ: 6,75

 

3) Дробно-рациональная функция

Пример задания

На рисунке изображён график функции вида  где числа a, b и c — целые. Найдите 

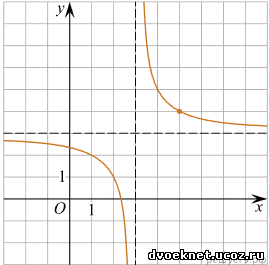
Решение. Для этого вида функций стоит обратить внимание на асимптоты графика.

Вертикальная асимптота х = 3 - это значение переменной х, при которой знаменатель дроби обращается в ноль. 

x + b = 0, x = 3, b = -3  

Горизонтальная асимптота у = 3 - это то значение функции, к которому стремится f(x). Так как значение дроби стремится к нулю при бесконечно больших значениях х, то значение функции f(x) стремится к с. То есть горизонтальная асимптота - это значение с, с = 3.

Остается подставить в формулу функции значения b = -3, c = 3 и координату одной точки графика, чтобы найти значение параметра а.

а = 2, f(-13) = 2,875

Ответ: 2,875

 

Еще проще в решении задачи следующего типа:

На рисунке изображён график функции вида  где числа a, b и c — целые. Найдите c.

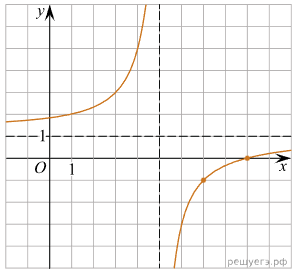
Так как параметр с входит в знаменатель дроби, то достаточно воспользоваться свойством вертикальной асимптоты: при х = 5 знаменатель дроби равен нулю. 

5 + с = 0, с = -5

Ответ: -5

Если нужно найти какой-либо другой параметр или значение функции в определенной точке, то оставшиеся параметры легко найти с помощью системы уравнений, подставив в функцию координаты двух точек графика, находящихся в узлах клетки, и параметра с.

 

4) Функция, содержащая модуль

Пример задания

На рисунке изображён график функции вида  где числа a, b, c и d — целые. Найдите корень уравнения 

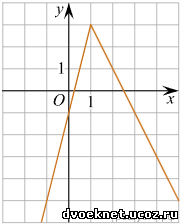
Несмотря на страшный вид этого задания, решается оно устно, одним взглядом на график (метод одного взгляда))))

Разберемся с графиком. Почему он "ломается" в точке (1; 3)? Вспомним, как раскрывается модуль. 

1) При bx +c > 0 |bx + c| = bx + c 

2) При bx +c < 0 |bx + c| = -bx - c 

3) При bx +c = 0 |bx + c| = 0

Первые два случая раскрытия модуля дадут левую и правую веточки графика, а третий случай - точку перелома графика.

То есть, в точке перелома графика  bx +c = 0. В этом и содержится идея решения задач подобного типа. 

В точке перелома графика модуль равен нулю!

Значит, корнем уравнения bx +c = 0 будет абсцисса точки перелома графика: х = 2.

Ответ: 2

 

Сложнее решить уравнение ax + d = 0

Пример задания.

На рисунке изображён график функции вида  где числа a, b, c и d — целые. Найдите корень уравнения 

Решение. Вспомним про секреточку: в точке перелома графика (1;3) модуль равен нулю! То есть, можно перейти к следующей системе уравнений:

b + c = 0                  c = -b

a + d = 3                d = 3 - a

Подставим найденные значения c и d, а также координаты двух точек графика (0;-1) и (3;-1) в формулу функции

-1 = 0 - |0 - b| + 3 - a                  a + |b| = 4                    a + |b| = 4                  a + |b| = 4                      a = 1               

-1 = 3a - |3b - b| + 3 - a              2a - 2|b| = -4                a - |b| = -2                  2a = 2                           |b| = 3

d = 3 - a = 2.

Значения b и с составляют пары (3; -3) и (-3; 3), но они не нужны для дальнейшего решения.

Решим уравнение ax + d = 0

x + 2 = 0

x = -2

Ответ: -2

 

Встретилось одно задание, в котором точка перелома не попадает на узел клетки.

На рисунке изображён график функции вида  где числа a, b, c и d — целые. Найдите корень уравнения 

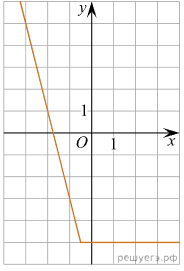
Во-первых, нужно найти абсциссу точки перелома графика. Найти ее можно как точку пересечения убывающей функции  y = kx + m и прямой у= -5. Составим уравнение убывающей функции. 

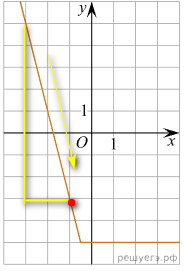
Коэффициент k найдем по графику убывающей линейной функции: k = - 4. Значение параметра m  вычислим, подставив в формулу  y = kx + m координату точки (-1; -3)

-4*(-1) + m = -3

m + 4 = -3

m = -7

Значит, убывающая линейная функция описывается формулой у = -4х - 7. Найдем точку пересечения этой функции с прямой у = -5

-4х - 7 = -5

-4х = 2

х = -0,5

Значит, координата точки перелома графика (-0,5; -5). 

Дальше решаем по алгоритму: в точке перелома графика bx + c = 0, ax + d = -5.

-0.5b + c = 0          c = 0.5b

-0.5a + d = -5          d = 0.5a - 5

Подставим значения параметров с и d, а также координаты точек графика (-1; -3) и (1; -5) в формулу функции:

-a + |-b + 0.5b| + 0.5a - 5 = -3               -0.5a + |-0.5b| = 2               -a + |b| = 4               |b| = 4 + a

a + |b + 0.5b| + 0.5a - 5 = -5                   1.5a + |1.5b| = 0                 a + |b| = 0               a + 4 + a = 0                2a = -4               a = -2

d = 0.5a - 5 = -1 - 5 = -6

Теперь можно подставить значения а и b в уравнение ax + b = 0 и вычислим значение х

-2х - 6 = 0

-2х = 6

х = -3 

Ответ: -3 

 

5) Тригонометрическая функция

6) Смешанная функция