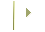Теорема Менелая

Элементы доказательства теоремы Менелая.

1. Дополнительное построение СЕ || AB

2. ∠1 = ∠2 и ∠3 = ∠4 ⇒ ΔECK ∼ ΔMAK ⇒ EC/MA = CK/AK = EK/MK

3. ∠5 = ∠6 и ∠7 = ∠8 ⇒ ΔECN ∼ ΔMBN ⇒ EC/MB = CN/BN = EN/MN

4. Из пункта 2. получаем: EC = (CK/AK) ·MA ⇒ EC/MB = (CK/AK) · (MA/MB) = CN/BN, последнее равенство получено из пункта 3 ;

5. Переписав последнее равенство в 4-ом пункте получаем: (CK/AK) · (MA/MB) · (BN/CN) = 1

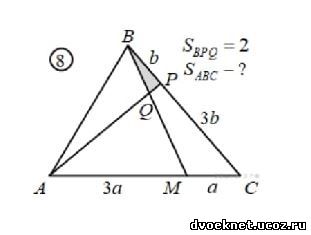
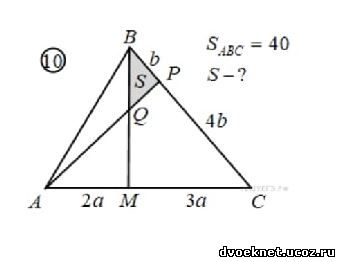
Задачи на ПОСТРОЕНИЕ и ВЫЧИСЛЕНИЕ ОТНОШЕНИЙ ОТРЕЗКОВ

1.1 Точка M лежит на ребре AB треугольной пирамиды ABCD, причём AM:MB=1:2.

a) Постройте сечение пирамиды плоскостью, проходящей через точку М и середины рёбер BC и AD.

6) B каком отношении плоскость сечения делит ребро CD?

1.2. Точка М —середина ребра AD треугольной пирамиды ABCD. Точки К H L лежат на прямых AB H AC соответственно, причём B—середина отрезка AK, а С — середина отрезка AL.

а) Постройте сечение пирамиды плоскостью, проходящей через точки M, K H L.

6) B каком отношении плоскость сечения делит ребро BD?

1.3. Точки M H N —середины рёбер соответственно AB H BC параллелепипеда ABCDA1B1C1D1 .

a) Постройте сечение параллелепипеда плоскостью, проходящей через точки М, N и D1.

6) B каком отношении плоскость сечения делит ребро 14311?

1.4. Точка M — середина ребра CD параллелепгшедаАВСБА1В1С1П1.

а) Постройте сечение параллелепипеда плоскостью, проходящей через точки М, Al H С,.

6) Пусть секущая плоскость пересекает прямую DD1 B точке Р. Найдите отношение PD : РПГ

1.5. Основание пирамиды SABCD — параллелограмм ABCD с цен- тром 0. Точка М лежит на отрезке SO, причём ОМ :MS = 1 :2.

a) Постройте сечение пирамиды плоскостью, проходящей через прямую AM параллельно прямой BD.

6) B каком отношении плоскость сечения делит ребро SC?

1.6. Основание пирамиды SABCD —llapaJIJIf'JIOI'pah[M ABCD с цен- тром 0. Точка М — середина отрезка A0.

a) Постройте сечение пирамиды плоскостью, проходящей через точку М параллельно прямым SA H ВВ.

6) B каком отношении плоскость сечения делит ребро SC? 1.?. Точки M H N —середииы рёбер соответственно CC1 H AB тре- угольной призмы АВСА1В1С1.