Координатно-векторный метод решения задач

Теория

Задачи для практики

Основные формулы

Если в пространстве заданы две точки А(х₁;у₁;z₁) и B(x₂;y₂;z₂), то вектор  имеет координаты

Длина вектора АВ вычисляется по формуле

Скалярное произведение векторов  и  можно вычислить двумя способами:

Из этих двух формул следует формула вычисления угла межу прямыми:

Уравнение плоскости имеет вид ax+by+cz+d=0, где {a;b;c} – координаты вектора нормали к плоскости, (x;y;z) – координаты точек плоскости.

Уравнение плоскости также может быть представлено в виде a(x-x₀) +b(y-y₀)+c(z-z₀)=0, где (x₀;y₀;z₀) – координата точки, принадлежащей плоскости.

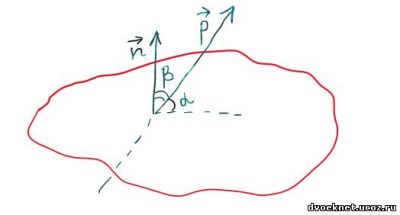
Угол между прямой и плоскостью вычисляется как угол между направляющим вектором прямой и вектором нормали плоскости

 

 

Расстояние ρ от точки М (x₀;y₀;z₀) до плоскости ax+by+cz+d=0 вычисляется по формуле

где  – вектор нормали плоскости.

Угол между плоскостями вычисляется как угол между векторами нормали к этим плоскостям. 

Задачи (Кагаполов, Бунеева)

1. В основании пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 2, ВС = 1. Точка М – середина ребра АВ. Боковые ребра пирамиды имеют одинаковую длину. Высота пирамиды равна . Через прямую ВМ параллельно прямой SA проходит плоскость α. Найдите расстояние от вершины С до плоскости α.

Ответ: 1.

 

2. Ребро куба ABCDA₁B₁C₁D₁равно 1. Точка М – середина ребра AD. Через точку N – середину отрезка В₁М – перпендикулярно прямой В₁М проведена плоскость α. Найдите расстояние от центра куба до плоскости α.

Ответ:

 

3. В основании прямой треугольной призмы ABCA₁B₁C₁ лежит правильный треугольник АВС со стороной 2, боковые ребра равны . Точки M. N. P – середины ребер ВС, СС1, А1С1 соответственно. Плоскость α проходить через точки M. N. P. Найдите расстояние от точки А до плоскости α.

Ответ: